back
3D to 2D projection
Tutorial about projecting 3D points to a 2D screen


by Crisp/Planet Jazz (april 1999)
corrections by Scout (*) (may 1999)

Introduction

This tutorial is aimed at explaining you how you can project a 3 dimensional point to a 2 dimensional plane (which in most cases will be the screen). This is the absolute basics you have to know before trying to code 3D effects. Most of you will probably already know the most oftenly used formulas by heart, but it is also important to know how those formula's can be derived.

The idea behind it all

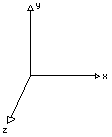
We will be working in a 3D space, with a right-handed base. This means that if you take your right hand and point your thumb in the direction of the X-axis, your ring- finger in the direction of the Y-axis, that the Z-axis will point straight up your hand-palm, as shown in the figure below:

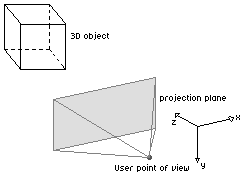
The user's point of view will be represented by a point in this 3D space. From this point, the user has a certain "view" on our 3D world. This view is drawn below as the pyramid. All ray of lights that pass this "pyramid" will originate from objects that the user sees. When they pass this pyramid, they also pass the front plane. In the end, the whole 3D to 2D projection will be about projection the entire 3D world on that plane in front of the pyramid (coloured grey in the figures). Imagine we want to project a cube on a plane. If we want to draw the situation, it would look somewhat like this (note that the base we use has been rotated a bit):

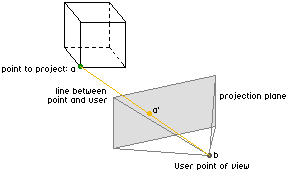
The projection plane will in the end be the screen that the user sees. If we want to project a point of our cube on this plane according to the user's view, we'll need to intersect the line (= ray of light) between the point to project and the user's point of view with our projection plane. Let's call the point we want to project a, and the user's point of view b. The line [ab] will intersect our projection plane, and the intersection point will be called a':

This a' will have the coordinates we are looking for. So let's bring in the math to find the coordinates of this a'.

The mathematical approach

Since we are working in a 3 dimensional space, all points are represented by three co-ordinates (the x-coordinate, the y-coordinate and the z-coordinate). Our point a from the cube will have three coordinates, let's call them (x,y,z). To make the calculations a bit easier, we'll put the user in the point zero (exactly where the user belongs :). The point a' that we are looking for will have the coordinates (u,v,w).

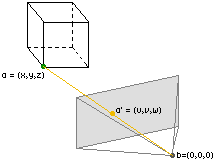
First of all, we'll need to define the plane we want to project everything on. The cartesian equation of a plane is z=value, where value is the offset of the plane (note that this z has nothing to do with the z-coordinate of our point a!). Since computers can work very easily with powers of 2, we'll use the plane z=256 as the projection plane (this means that the third coordinate of all points in the projection plane are 256). There's also another reason why we choose 256, try changing the value to a bigger or lower value to see the result!. If the third coordinate of all points in the plane equals 256, then the coordinates of our point a' will look like (u,v,256) (the point a' has to lie in our projection plane, and all third coordinates of points in that plane are 256). This means that we only have to look for two more coordinates (u and v).

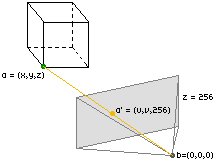
We can get those two coordinates by calculating the intersection point of the line [ab] with the plane z=256. First we need to define the line between two points: mathematically, the line [ab] is the collection of all points between the point a and the point b:

[ab] = {all points between a and b}

Without going into too much detail about the linear algebra, I'll tell you that the equation for a line is given as:

[ab] = b + c * (a - b)

where c can be any real value. We just described that all points have three coordinates, and a = (x,y,z), b = (0,0,0), so we could also say that the equation is:

[ab] = (0,0,0) + c * (x - 0, y - 0, z - 0)

[ab] = (0,0,0) + c * (x, y, z)

[ab] = (0 + c*x , 0 + c*y , 0 + c*z)

This means that a point (e,f,g) is on the line [ab] when a certain value c exists so that:

(e,f,g) = ( c*x , c*y , c*z )

Our point a' = (u,v,256) also lies on the line [ab], so we can say that there is a certain value for c so that:

(u,v,256) = ( c*x, c*y, c*z )

This means that:

u = c * x
v = c * y
256 = c * z

This last equation allows us to find the value for c:

c = 256 / z

So the coordinates of the point a' = (u,v,256) become:

(u,v,256) = ( x * 256 / z , y * 256 / z , 256 )

Or, if we look at the coordinates in the plane z=256:

u = x * 256 / z
v = y * 256 / z


These are the basic projection formulas to convert (almost) every point in a 3 dimensional space to a 2 dimensional plane. As you can see, the feeling of "depth" is accomplished by dividing by the z-value for every point. (*)

Note: This formula is only valid for points that have a z-coordinate greater than zero. (Points with a z-coordinate of zero are not possible to project, and points with a negative z-coordinate project to completely meaningless coordinates; rendering such points could potentially corrupt innocent memory and is generally not a good idea.) Hence, do not forget to leave out points that have a zero or negative or z-coordinate! (*)